1071. Greatest Common Divisor of Strings

• Why you may want to read this note
• Problem
• Solution1 O(min(m,n) * (m + n)) & O(max(m, n))
• Solution2 O(m+n) & O(m+n)

Why you may want to read this note

As a Software Engineer at Microsoft I didn’t do LeetCode interview questions for a long time already. Now I’m refreshing my skills in algorithm questions and these set of articles are for myself in future and for whoever is solving it right now.

We are going to discuss the thinking process, insights, worse/better approaches, complexity analysis

Questions list: https://leetcode.com/studyplan/leetcode-75/

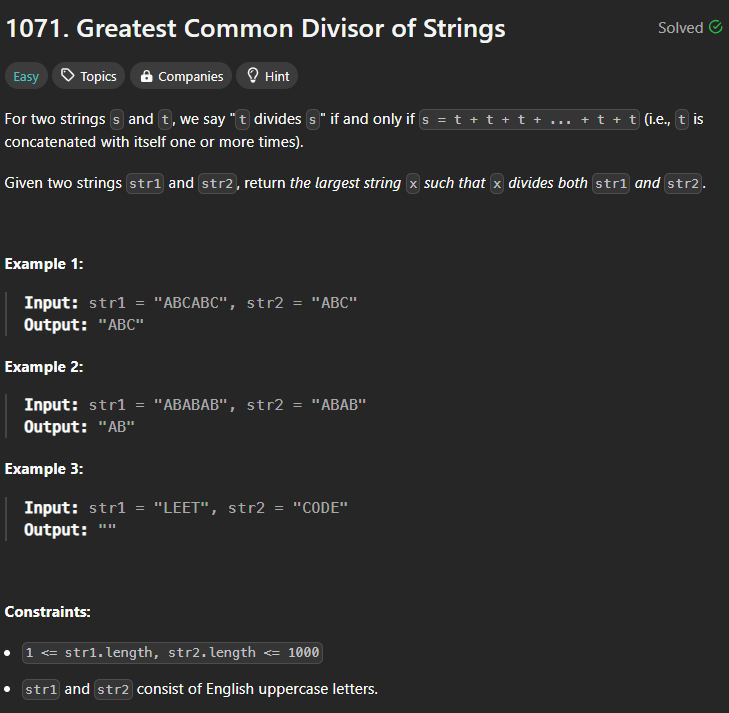
The problem is 1071. Greatest Common Divisor of Strings

Problem

Solution1 O(min(m,n) * (m + n)) & O(max(m, n))

We want to find the greatest divisor of 2 strings. The naive approach is already stated in the problem: s = t + t + t +t … We just take the common divisor string candidate and try to concatenate it until it becomes the final string we are checking.

The greatest candidate should start from the smallest of the 2 strings: e.g. AAAA, AA, candidate = AA, as the same applies in math GCD(15,10) cannot be bigger than 10.

We start with the smallest of str1 and str2 and try every prefix from the biggest to the smallest until we find that it can add up to str1 and str2.

One optimization that can be applied: sometimes prefix length is not divisible (has reminder when divided) - then we for sure know it cannot be divisor, e.g. str1=”ABAB”, str2=”ABABAB”, candidate!=”ABA” as 6%3=0, but 4%3=1

var gcdOfStrings = function(str1, str2) {
    let minLen = Math.min(str1.length, str2.length)

    for (let prefixLen = minLen; prefixLen > 0; prefixLen--) {
        let prefix = str1.slice(0, prefixLen)

        if (str1.length % prefix.length !== 0 || str2.length % prefix.length !== 0) {
            continue;
        }

        let isGcd = isDivisible(str1, prefix) && isDivisible(str2, prefix)
        if (isGcd) {
            return prefix
        }
    }

    return ''

    function isDivisible(fullString, candidate) {
        let stringToCheck = candidate;

        while (stringToCheck.length <= fullString.length) {
            if (stringToCheck === fullString) {
                return true
            }
            stringToCheck += candidate
        }

        return false
    }
};

Runtime Complexity: O(min(m,n) * 2(m + n)), O(min(m,n)) - taking every prefix, O(2(m+n)) checking whether str1 and str2 can be made by candidate.

We are omitting concatenation complexity, as mostly, since strings are immutable concatenation will take O(s1+s2) time. However optimization can be done over array of chars

Space Complexity: O(max(m, n)), as we are concatenating candidate up to biggest of str1 str2

Solution2 O(m+n) & O(m+n)

I’ll be honest with you I didn’t come up with this solution, also people voted for this question to be Medium:

We can think about it more mathematically.

Let’s assume that 2 strings have a common divisor, which means there is some prefix that can add up to both of them by concatenating long enough. In this case the concatenation of 2 final strings should give the result the same result: [ABC][ABC][ABC]’ + ‘[ABC][ABC]’ === ‘[ABC][ABC]’ + ‘[ABC][ABC][ABC] same as 9*6 == 6*9.

After checking this, we know for sure that there is a number X (str1.length), Y(str2.length) and they for sure have a common divisor. Then we can just mathematically find the greatest common divisor of these numbers and this will be the length of their word common divisor

For the greatest common divisor we will use the Euclidean algorithm.

var gcdOfStrings = function(str1, str2) {
    if (str1 + str2 !== str2 + str1) {
        return ""
    }

    let greatest = gcd(str1.length, str2.length)
    return str1.slice(0, greatest)

    function gcd(num1, num2) {
        if (num1 < num2) {
            return gcd(num2, num1)
        }

        let reminder = num1 % num2
        if (reminder === 0) {
            return num2;
        }

        return gcd(num2, reminder)
    }
};

Runtime Complexity: O(m+n) = O(m+n) to concatenate the strings and compare them + O(log(max(m,n))) for Euclidean algo, can be formally proven inductively by moving to Fibonacci number.

In our case it does not matter, we are interested in Big O notation, and concatenation of the strings is already bigger than GCD, so we can omit it

Space Complexity: O(m + n), as concatenated strings