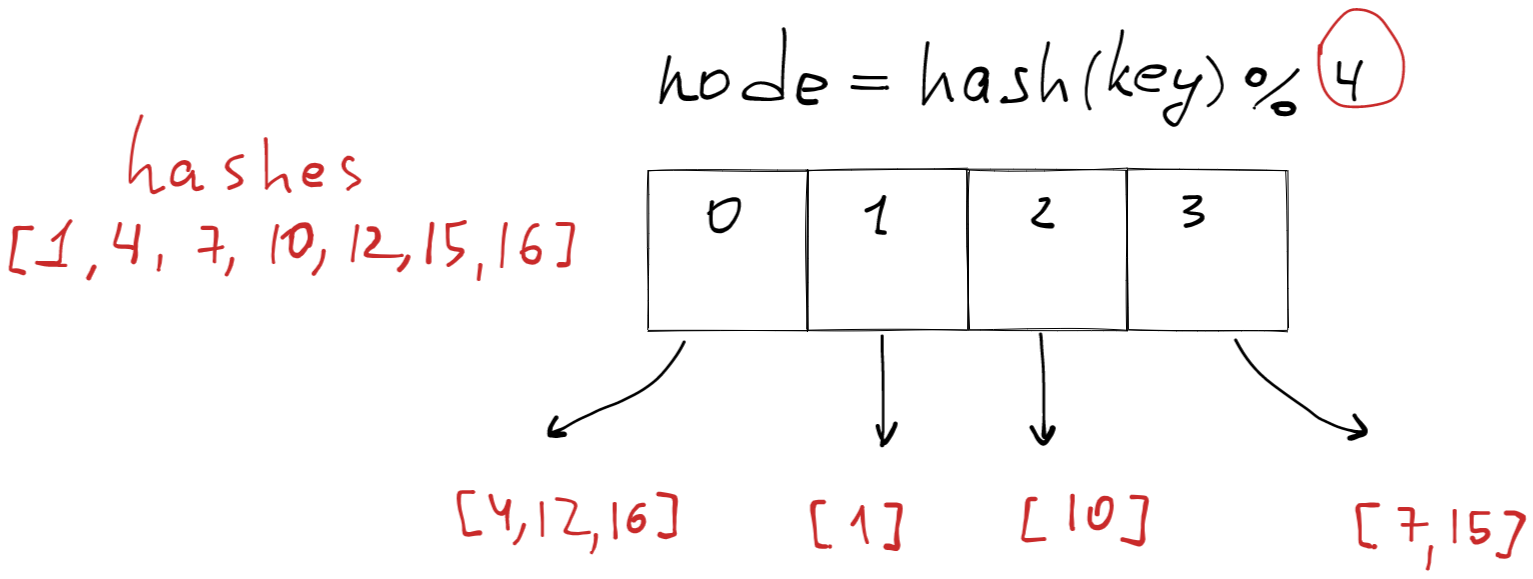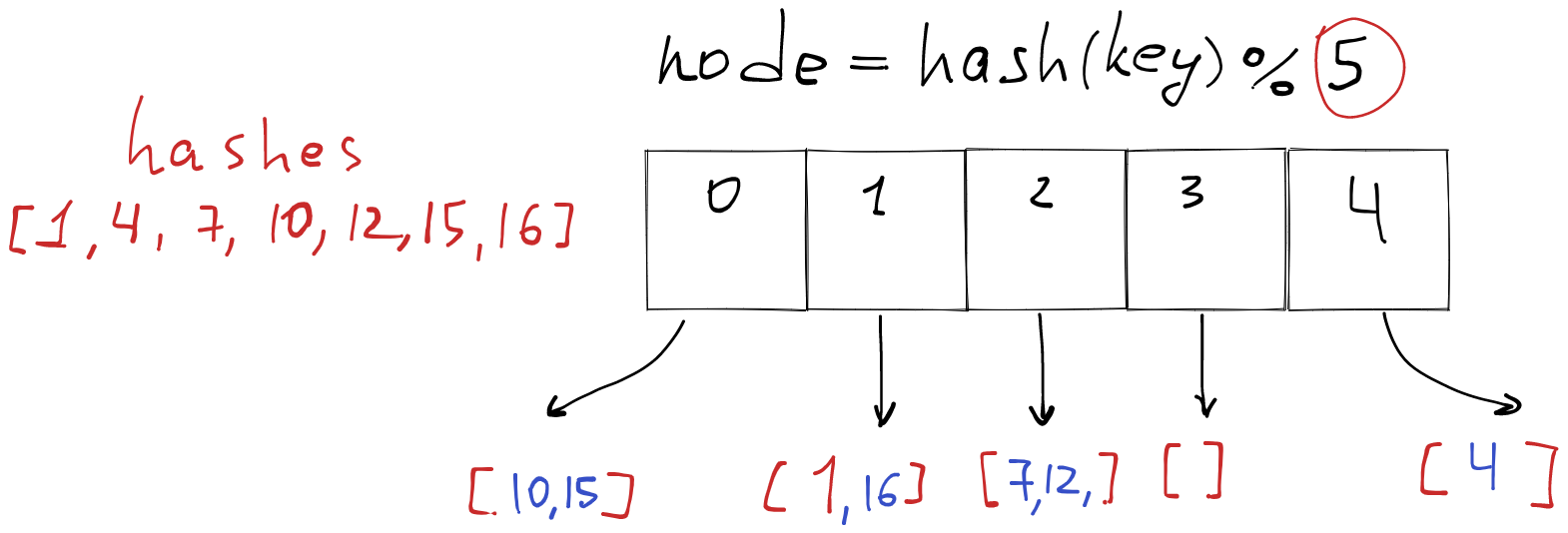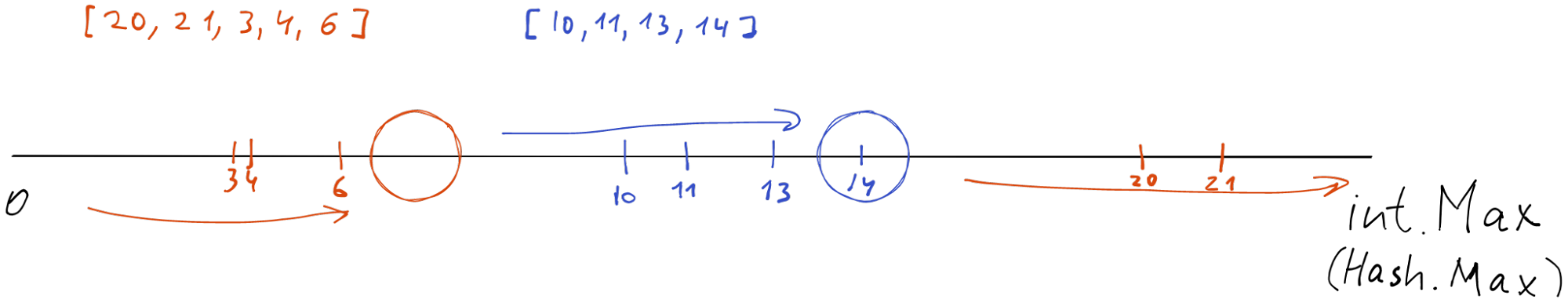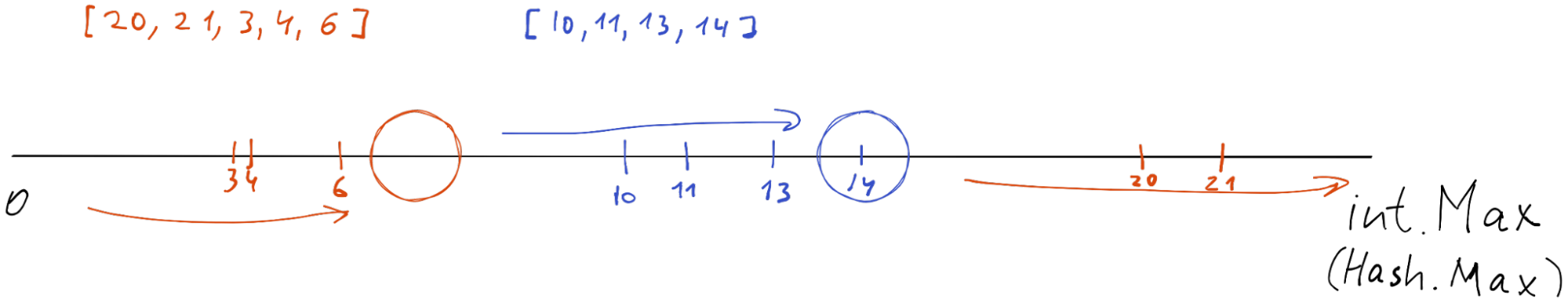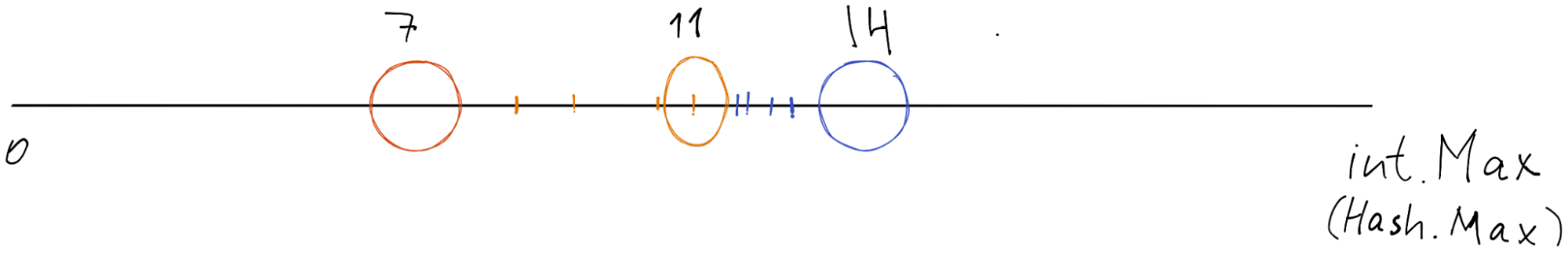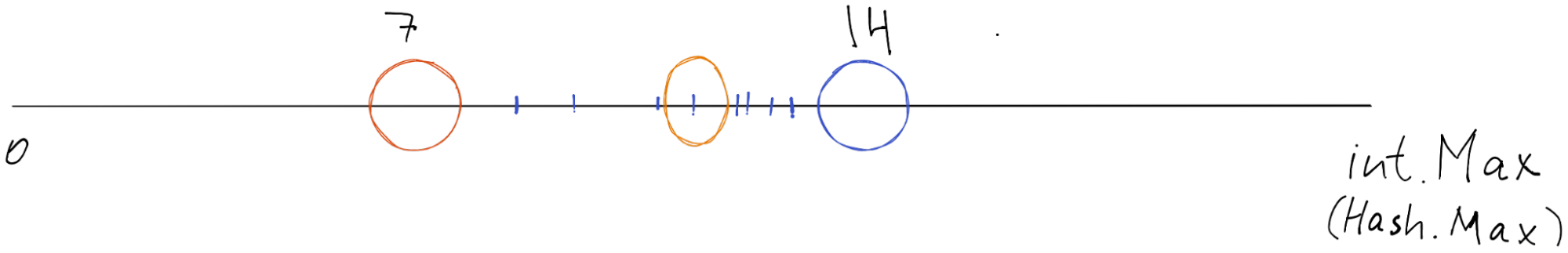Why you may want to read this article
In this article, we will discuss a technique designed to work with partitioned data called Consistent Hashing. This is a specific technique of spreading the load between servers when using Partitioning in the way, that rebalancing does not require moving 90%+ of all elements. The applications of Consistent Hashing could be distributed caches in partitioned databases.
Consistent hashing is used in Dynamo, Apache Cassandra, Riak [1], and it seems from design docs that MongoDB supports it as well [2].
The simplified implementation of Consistent hashing with auto-rebalancing will be discussed in the next article. This article is about the algorithm itself, its complexity, and its overview.
Why Consistent hashing
One machine hash table
You have most probably heard about the hash table [3]. It is a key-value data structure that provides O(1) amortized complexity for getting and adding key-value pairs.
Usually hash table is represented in the following way:
- There is an array that stores values. You can access this array by index
- To know the index you hash the key that will produce some number and perform a modulo operation by the length of an array. With this index, you go to array and get your item.
- Since typically array size is less than the range of all possible hashed keys - you will end up having collisions (when different keys are mapped to the same index). We will not discuss this.
This is what get/add functions look like (simplified):
function get(key) {
var index = hash(key) % array.size;
return array[index];
}
function add(key, value) {
var index = hash(key) % array.size;
array[index] = value;
}
Multiple machines hash table
One machine hash table works until there are more key/value pairs than it can handle. Since vertical scaling always has limitations and is very expensive we reject this as an option.
In the context of the overloaded node we can differentiate 2 main dimensions:
Memory-overloaded node: the node that does not have enough capacity in terms of memory to handle all the data.Request-overloaded node: the node that does not have enough capacity to process all incoming requests.
When we have a Memory-overloaded node problem (which is the case) the one obvious solution is to use partitioning [4]. Partitioning [5] is a technique that splits data among machines so that each machine is responsible for handling a subset of data. Sometimes partitioning solves Request-overloaded node problem as well.
Since we are talking about Distributed Hash Table, Partition by key range does not fit our needs [6]. The natural approach will be Partitioning by Hash of Key [7] because we do not have range queries, and we already have a hash of the key.
Assume we have multiple nodes and we want them to maintain their own hashtable that will be responsible for a subset of overall data. It is very important to choose the strategy by which we pick the node based on the key hash.
The naive approach
We can use the modulo operation that we used in One machine hash table approach.
Let’s say we have 4 nodes in the array. Then for each key, we will use this formula to map the key to the node.
let nodeIndex = hash(key) % array.length
let node = array[nodeIndex];
Imagine we have 4 nodes [0, 1, 2, 3].
At some point, we have added the elements to those nodes based on the above formula, elements: [1, 4, 7, 10, 12, 15, 16]
1 % 4 = 1, 4 % 4 = 0, 7 % 4 = 3…
If we have a static amount of nodes - this strategy works well.
Unfortunately, in Distributed Systems environment, we cannot rely on a static amount of nodes. At some point, some nodes could be memory-overloaded and we might need to add new nodes or remove existing ones.
The problem with this approach is that whenever we change a number of nodes - we end up shuffling 90%+ elements.
Let’s say we added 5th node with index 4.
The numbers that changed the server have a blue color. Only 1 item left on the same server that it was before we added one more node.
1 % 5 = 1, 4 % 5 = 4, 7 % 5 = 2…
This problem also was described in the original paper about Consistent Hashing by David Karger [8].
Consistent hashing is designed to solve this problem of rebalancing.
Consistent Hashing
The initial paper that mentioned Consistent Hashing was done by David Karger “Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web” [8].
It is hard to read if you don’t know the concept in the first place. So I will use only some of the screenshots from the paper.
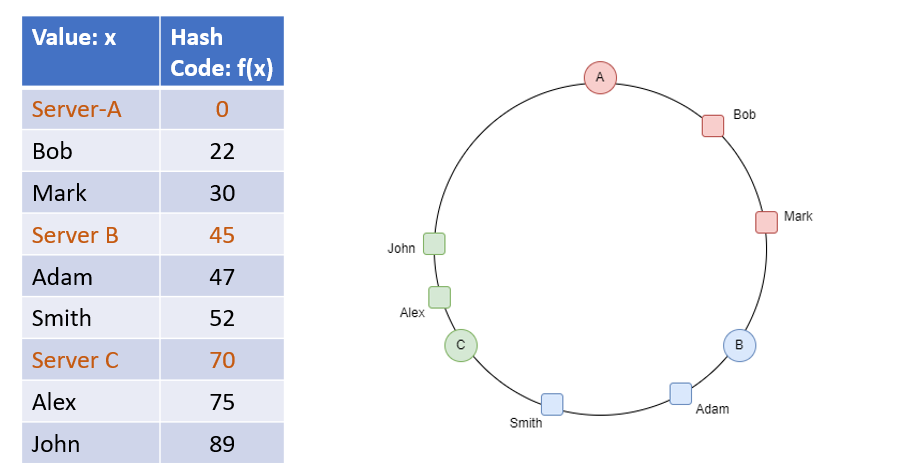
Circle representation
Usually, we have the following representation:
There is 360-degree ring, that contains nodes placed on it along with hash values. There are items that are assigned to nodes.
The circle with degrees confused me when I was learning. Because it is rarely explained how to map hash value to degrees, and how to represent the circle with degrees in the code.
Number line representation
Since almost all implementations use the raw hash value as position, usually we are bounded by the maximum value that the hash function could produce, typically it is long (64-bit number). In our implementation, it is int(32-bit number).
We cannot get anything larger than 32-bit number from the hash function, so int32.MaxValue is our maximum hash value. We can represent our hash value space from zero to int32.MaxValue. Then we can put our nodes and items into this space line.
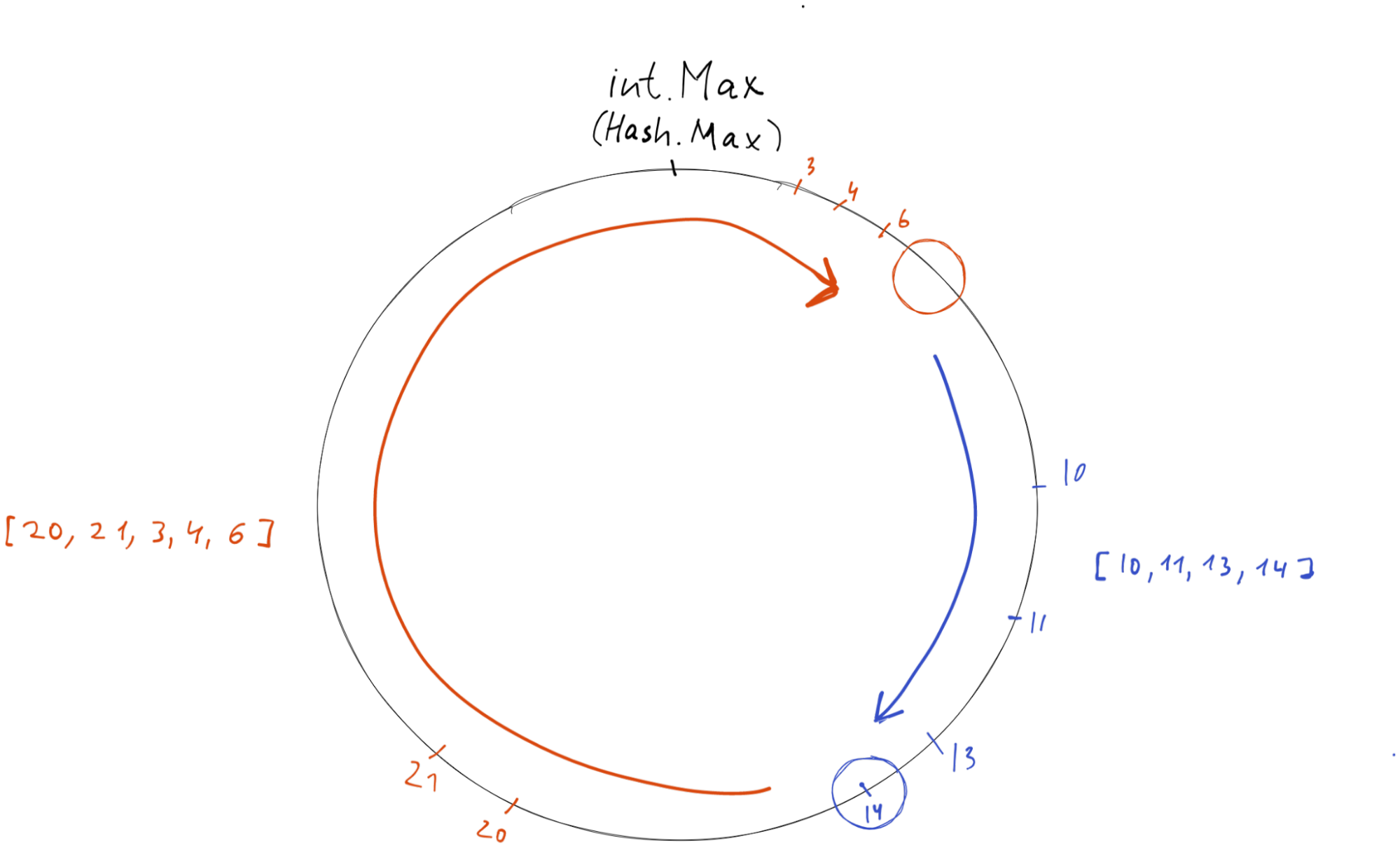
We still can represent it as a circle:
Even more, we still can do mapping hashvalue -> circle degree. For that, we need to convert the hash value using that formula: hashvalue * (360/int.Max). But it is unnecessary overhead, so let’s stick with hash values themselves.
Algorithm
Terminology & prerequisites
In our implementation:
1. We name physical node as a physically separate server, so no 2 physical nodes can have the same domain. Still, internally, they can physically be served from 1 server, using virtualization, for example, as 2 different docker containers with 2 different docker hosts.
We name virtual node - as some separate application that can be run on any physical server (physical node). One physical node can run multiple virtual nodes.
Technically speaking virtual node should have a unique port (as application boundary) per physical node, and physical node should have unique domain name or ip (as machine boundary).
We leave implementation details of managing mapping of physical node -> virtual node beyond this article. Usually, virtual nodes are needed to create some pre-setup for a cluster, and to balance the load between weaker and stronger physical nodes.
Whenever we are talking about the node we mean virtual node.
2. We name cluster as a whole system consisting of all physical and virtual nodes.
3. In a real implementation apart from child nodes (virtual nodes) that actually handle cache partitions - there are Load Balancers that are responsible for routing traffic to specific child node for get/set operation, and Master that is responsible for rebalancing. In the next article, I will show and explain why we need Load Balancer and Master.
When explaining the algorithm all those additional entities (services) will not be mentioned.
4. We name Hash Ring the hash value space (see Number line representation).
Presetup
In our algorithm, we start with at least 1 node in the cluster.
As far as I know usually the cluster starts with quite a lot of initialized beforehand nodes depending on the load. Because rebalancing when the cluster is running is more expensive than having a preset cluster with ready nodes.
How to initialize your cluster depending on the expected load - is another topic, we will not cover in this article.
Explanation
The main invariant of the Hash Ring is simple: each item (key hash) should be handled and stored by the nearest node (right most in our implementation).
[10,11,13,14] have the blue nearest rightmost node and are stored by it. [20, 21, 3, 4, 6] have the orange nearest rightmost node and are stored/handled by it.
From Consistent Hashing by David Karger [8]:
1. Add Node
Before adding and getting key-value pairs we need to add nodes to our Hash Ring. There are different techniques how to calculate the position on the ring for the node.
In our algorithm, we will just calculate the hash of the full URL of node trying to evenly distribute all preset nodes.
2. Add Value
When we want to add key-value to our Hash Ring:
1. We calculate a key hash
2. Having that key hash we calculate the nearest node to the right
3. Send add request to that node with key-value
4. The node adds value by key hash to the internal hashtable
Based on the picture above every number that is greater than 7 and less than or equal to 14 goes to the blue node. Other key hashes go to the red node.
Internally (we will discuss this in the next article) we keep sorted list of all nodes in the Hash Ring. Whenever we have some key hash - we apply binary search variation to the sorted list to pick up the nearest right node. This operation costs us O(logm) where m is the count of all nodes. Usually, it is not that big a number.
Example from my implementation of Consistent Hashing
public uint BinarySearchRightMostNode(IList<uint> nodePositions, uint keyPosition)
{
// in case keyPosition is bigger than MaxValue (if we consider to use real 360 degree circle or any other scale)
// we should adjust it to max value of ring
keyPosition = keyPosition % MaxValue;
var start = 0;
var end = nodePositions.Count - 1;
while (start != end)
{
var mid = ((end - start) / 2) + start;
if (keyPosition <= nodePositions[mid])
{
end = mid;
}
else
{
start = mid + 1;
}
}
var nodePosition = nodePositions[start];
// if your key is after node but before MaxHashValue - we return first node (because it is hash circle)
if (keyPosition > nodePosition)
{
return nodePositions[0];
}
return nodePosition;
}
3. Get Value
When we want to get value by key from our Hash Ring:
1. We calculate a key hash
2. Having that key hash we calculate the nearest node to the right
3. Send get request to that node
4. The node looks up the internal hashtable for the value by the key hash and returns it
4. Rebalance
Each node contains Max Items count. If the count of items reaches Max Items count - the node emits a notification to Master Service that starts rebalancing.
The rebalancing algorithm consists of the following steps:
1. Create new node
2. Put the newly created node before the overloaded
3. Transfer the first half of the elements to the newly created node from the overloaded one
4. Delete the first half of the element from the overloaded node.
How to split Hash Ring space between current and previous node?
The intuition could be to cut the hash value space between the current and previous nodes on 2 halves. Put the newly created node in the middle. Then transfer the first half to a new node, and remove the first half from the overloaded node.
Unfortunately, this might not work well. Consider this case:
It is possible that the right part of the Hash Ring (green underscore) has more items (6) than the left (orange underscore) one (2).
Therefore, each node keeps key/values sorted. When we rebalance - we put a new node exactly on the middle item, in our case it is 8 / 2 = 4th item.
It would look like this:
Since we have 8 items, we cut our space on the 4th item and put our newly created node there. Then we need to assign the first half (orange underscore) to the orange node. And delete the first half (orange underscore) from the blue one.
From Consistent Hashing by David Karger [8]:
From the observation, we can conclude, that each time we rebalance the node, we are moving at most n/m items, where n - is the count of all items, m - is the count of all nodes.
5. Removing node
The removal of unused or broken node will be done the other way around.
1. We transfer all elements to the next node (in this case blue)
2. We drop the orange node from the ring.
From the observation, we can conclude, that each time we removing the node, we are moving at most n/m items, where n - is the count of all items, m - is the count of all nodes.
Corner case
We need to keep in mind that this Number line is actually endless like a circle. So whenever we are adding or getting key-value that are greater than 14 - they should go to the node on the 7th index (picture above).
As you can see, the 20 and 21 key hash belong to the orange node.
Summary
In this article, we considered Consistent Hashing as a Partitioning approach that allows cheap rebalancing in terms of shuffling items between the nodes.
We can represent Hashing Ring as Circle and as a Nubmer line. The number line is closer to real implementation.
The naive approach with key hash mod numberOfNodes does not work well in Distributed Environment.
The Consistent Hashing algorithm moves at most n/m items, where n - number of all items, m - number of nodes.
We have 2 types of nodes: physical which corresponds to a separate server or virtual server (which has a unique domain name in the cluster), and virtual which corresponds to one of the applications inside the physical node.
We considered the algorithm of adding/removing of virtual node to the Hash Ring, adding/getting key-value from the node. The lookup of the node in Consistent Hashing takes O(log m) where m is the count of all virtual nodes.
We reviewed parts of the original paper by David Karger about Consistent Hashing.
I am not that big expert in Distributed Systems, so I might be wrong in my assumptions. Please leave your feedback on my social media (About Section) and I will do corrections.
Thank you for your attention.
Please subscribe to my social media to not miss updates.: Instagram, Telegram
I’m talking about life as a Software Engineer at Microsoft.
Besides that, my projects:
Symptoms Diary: https://symptom-diary.com
Pet4Pet: https://pet-4-pet.com
References
[1] Wikipedia: Consistent hashing algorithm usages, https://en.wikipedia.org/wiki/Consistent_hashing#Examples
[2] MongoDB official documentation: https://www.mongodb.com/docs/manual/core/hashed-sharding/#hashed-sharding
[3] Wikipedia: Hash Table, https://en.wikipedia.org/wiki/Hash_table#
[4] Martin Kleppmann: “Designing Data-Intensive Applications”, pages 199-219, March 2017
[5] Wikipedia: Partition, https://en.wikipedia.org/wiki/Partition_(database)
[6] Martin Kleppmann: “Designing Data-Intensive Applications”, page 202, March 2017
[7] Martin Kleppmann: “Designing Data-Intensive Applications”, page 203, March 2017
[8] David Karger, Eric Lehman, Tom Leighton, Matthew Levine, Daniel Lewin, Rina Panigrahy: “Consistent hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web”, 4 paragraph, 1997
Diagrams file is here. Go to googlecloudcheatsheet.withgoogle.com/architecture and load this file.